These observations allow one to formalize the definition of reflection: a reflection is an involutive isometry of an Euclidean space whose set of fixed points is an affine subspace of codimension 1.
这些观察允许我们形式化反射

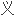 : 反射是欧
: 反射是欧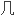 里得空间
里得空间

 等距同构,它
等距同构,它 不动点集
不动点集 是余维度为 1
是余维度为 1  仿射子空间。
仿射子空间。
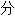
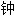 论文
论文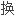 。
。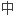 添加一个正则项,规定这些颜色只能进行仿射变
添加一个正则项,规定这些颜色只能进行仿射变 外标准的解决方案,在我们的例
外标准的解决方案,在我们的例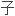
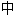
 ,本质上是使用缩放、旋转和剪切来保留点和平行线。
,本质上是使用缩放、旋转和剪切来保留点和平行线。


