This limits greatly the possible range of your factorial function.
这极大地限

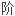
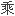

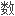
 可能范围。
可能范围。
声明:以上例句、词性分类均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
 汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版) 
 汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)  汗
汗 院:统计
院:统计 (视频版)
(视频版)