One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学中
 要求其解是正规或可对角化四元数矩阵的
要求其解是正规或可对角化四元数矩阵的 征值反问题。
征值反问题。
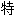 征值
征值One kind of inverse eigenvalue problems, whose solutions are required to be normal or diagonalizable matrices, is investigated in quaternionic quantum mechanics.
摘要本文研究了四元数量子力学中
 要求其解是正规或可对角化四元数矩阵的
要求其解是正规或可对角化四元数矩阵的 征值反问题。
征值反问题。
This paper discusses the structure, calculation of multiplication and power, eigenvalue and eigenvector, and diagonalizable problems of matrix of rank equal to 1.
摘要对秩等于1的矩阵的结构、乘法与乘幂运算、 征值与
征值与 征向量和对角化问题进行了讨论。
征向量和对角化问题进行了讨论。
Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
每个可见 征值符合操作
征值符合操作

 征向量,而相关的
征向量,而相关的 征值符合
征值符合 征值里的可见值。
征值里的可见值。
In the practical applications of highly nonnormal matrices, these theorems may be more useful than their generalized eigenvalue special cases and may provide more descriptive information.
在对高度非正规矩阵的研究应用中,这些定理将比它们的 例-广义
例-广义 征值定理更可靠,能提供更多的信息。
征值定理更可靠,能提供更多的信息。
声明:以上例句、词性分 均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。
均由互联网资源自动生成,部分未经过人工审核,其表达内容亦不代表本软件的观点;若发现问题,欢迎向我们指正。